| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:44 pon, 3. 1. 2011 Naslov: Postano: 15:44 pon, 3. 1. 2011 Naslov: |
    |
|
|
[quote="Lanek_"][latex]2.) \mu=4[/latex][/quote]
Od kud sad to? :/ Možeš li napisati postupak, jer inače ne mogu vidjeti tvoj tok misli? :) Kao i morniku, telepatija mi nije jača strana. :D
Zar mi ne vjeruješ? :D
[quote="pmli"]Trebalo bi ispasti 2-parametarsko rješenje za [latex]\mu = 7[/latex], a inače 1-parametarsko.[/quote]
Tada sam koristio Mathematicu, ali sad sam i "ručno" provjerio. ;)
Pažljivijim čitanjem sam primjetio nešto čudno u jednom starijem postu.
[quote="Lanek_"]i tak dobijem rjesenje sa 2 parametra, t i [latex]\mu[/latex][/quote]
[latex]\mu[/latex] možda zovemo parametrom, ali on nema apsolutno nikakve veze s parametrima rješenja sustava. Istina da će rješenje ovisiti o [latex]\mu[/latex], ali ako je [latex]\mu \neq 7[/latex], onda je rješenje doista jednoparametarsko, tj. dimenzija rješenja prostora pripadnog homogenog sustava je 1. Najbolje je [latex]\mu[/latex] shvatiti kao konstantu (aka. "proizvoljan, ali fiksan broj").
| Lanek_ (napisa): | 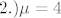 |
Od kud sad to?  Možeš li napisati postupak, jer inače ne mogu vidjeti tvoj tok misli? Možeš li napisati postupak, jer inače ne mogu vidjeti tvoj tok misli?  Kao i morniku, telepatija mi nije jača strana. Kao i morniku, telepatija mi nije jača strana. 
Zar mi ne vjeruješ? 
| pmli (napisa): | Trebalo bi ispasti 2-parametarsko rješenje za 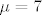 , a inače 1-parametarsko. , a inače 1-parametarsko. |
Tada sam koristio Mathematicu, ali sad sam i "ručno" provjerio. 
Pažljivijim čitanjem sam primjetio nešto čudno u jednom starijem postu.
| Lanek_ (napisa): | i tak dobijem rjesenje sa 2 parametra, t i 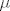 |
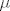 možda zovemo parametrom, ali on nema apsolutno nikakve veze s parametrima rješenja sustava. Istina da će rješenje ovisiti o možda zovemo parametrom, ali on nema apsolutno nikakve veze s parametrima rješenja sustava. Istina da će rješenje ovisiti o 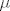 , ali ako je , ali ako je 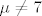 , onda je rješenje doista jednoparametarsko, tj. dimenzija rješenja prostora pripadnog homogenog sustava je 1. Najbolje je , onda je rješenje doista jednoparametarsko, tj. dimenzija rješenja prostora pripadnog homogenog sustava je 1. Najbolje je 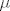 shvatiti kao konstantu (aka. "proizvoljan, ali fiksan broj"). shvatiti kao konstantu (aka. "proizvoljan, ali fiksan broj").
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
 Postano: 16:17 pon, 3. 1. 2011 Naslov: Postano: 16:17 pon, 3. 1. 2011 Naslov: |
    |
|
|
hmm, dobro evo postupak (nadala sam se da cu ga izbjec :evil: )
ovaj zadnji stupac su slobodni clanovi, sori ne znam kak se ona crta stavlja, ugl, prosirena matrica xD
[latex]\begin{pmatrix}
1 & 1 & 2 & 2 & 2\\
2& 3 &1 &3 &\mu \\
2& 1 & \mu & 5 & 1
\end{pmatrix}
\sim
\begin{pmatrix}
1 & 1 & 2 & 2 &2 \\
0 & 1 & -3 & -1&-4+\mu \\
0 & -1 & -4+\mu &1 & -3
\end{pmatrix}
\sim
\begin{pmatrix}
1 &1 & 2 & 2 & 2\\
0& 1 & -3 & -1 & -4+\mu \\
0&0 &-7+\mu &0 & -7+\mu
\end{pmatrix}[/latex]
otuda ta 3 rjesenja.
za [latex]\mu\neq7 ,\mu\neq4[/latex]
dobijem
[latex]
\begin{pmatrix}
1-\mu-3t\\
-1+\mu+t\\
1\\
t \\
\end{pmatrix}[/latex]
za [latex]\mu=7[/latex]
dobijem:
[latex]\begin{pmatrix}
-1-5s-3t\\
3+3s+t\\
s\\
t
\end{pmatrix}[/latex]
a za [latex]\mu=4[/latex] dobijem:
[latex]\begin{pmatrix}
-3-3t\\
t+3\\
1\\
t
\end{pmatrix}[/latex]
evo potrudila se i sve napisala. xD
hmm, dobro evo postupak (nadala sam se da cu ga izbjec  ) )
ovaj zadnji stupac su slobodni clanovi, sori ne znam kak se ona crta stavlja, ugl, prosirena matrica xD
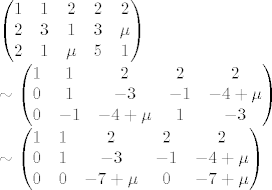
otuda ta 3 rjesenja.
za 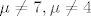
dobijem
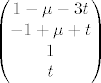
za 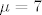
dobijem:
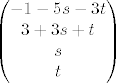
a za 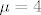 dobijem: dobijem:
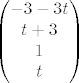
evo potrudila se i sve napisala. xD
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:58 pon, 3. 1. 2011 Naslov: Postano: 16:58 pon, 3. 1. 2011 Naslov: |
    |
|
|
[quote="Lanek_"]evo potrudila se i sve napisala. xD[/quote]
:karma:
Dobar ti je postupak, samo nema potrebe za slučajem [latex]\mu = 4[/latex]. Moj komentar u vezi zvanja [latex]\mu[/latex] parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš [latex]\mu = 4[/latex] u prvi slučaj, dobit ćeš isto što i u trećem. :)
[quote="Lanek_"]ovaj zadnji stupac su slobodni clanovi, sori ne znam kak se ona crta stavlja, ugl, prosirena matrica xD[/quote]
Ako te zanima, to se može riješiti okolinom array. Treba se samo dodati |. :) Ne znam kako napraviti da bude isprekidana. :?
[latex]\left[\begin{array}{cc|c}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right][/latex]
[code:1]\left[\begin{array}{cc|c}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right][/code:1]
| Lanek_ (napisa): | | evo potrudila se i sve napisala. xD |

Dobar ti je postupak, samo nema potrebe za slučajem 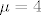 . Moj komentar u vezi zvanja . Moj komentar u vezi zvanja 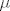 parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš 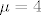 u prvi slučaj, dobit ćeš isto što i u trećem. u prvi slučaj, dobit ćeš isto što i u trećem. 
| Lanek_ (napisa): | | ovaj zadnji stupac su slobodni clanovi, sori ne znam kak se ona crta stavlja, ugl, prosirena matrica xD |
Ako te zanima, to se može riješiti okolinom array. Treba se samo dodati |.  Ne znam kako napraviti da bude isprekidana. Ne znam kako napraviti da bude isprekidana. 

| Kod: | \left[\begin{array}{cc|c}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right] |
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 17:13 pon, 3. 1. 2011 Naslov: Postano: 17:13 pon, 3. 1. 2011 Naslov: |
    |
|
|
Da se nadovezem na kolegu pmli-a, slucajeve razlikujes samo kad "postoji opasnost" da redak mnozis s 0 (primjerice s [latex]\mu - 7[/latex], sto je jednako 0 za [latex]\mu = 7[/latex]) sto najcesce mozes izbjeci da ni ne koristis tu tranformaciju, ili kad koristis tranformaciju mnozenja retka skalarom i dodavanje drugom... tu nije problem mnozenje s 0 (na kraju krajeva to nikako nebi ni utjecalo na sustav) vec dijeljenja s 0, npr. u tvojoj 3. matrici da bi ponistila 3. stupac moras 3. redak mnoziti redom s [latex]\frac{-2}{-7+\mu}[/latex], odnosno [latex]\frac{3}{-7+\mu}[/latex], sto ne smijes iz ocitih razloga ako je [latex]\mu = 7[/latex].
E sad sto se tice razlikovanja slucaja [latex]\mu = 4[/latex], ovdje nema potrebe za tim, jer zasto nebi mogao slobodni clan biti 0? Problem bi nastao da su svi ostali elementi retka jednaki 0, a slobodni clan razlicit od 0, tad sustav nebi imao rjesenje.
Da se nadovezem na kolegu pmli-a, slucajeve razlikujes samo kad "postoji opasnost" da redak mnozis s 0 (primjerice s 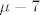 , sto je jednako 0 za , sto je jednako 0 za 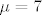 ) sto najcesce mozes izbjeci da ni ne koristis tu tranformaciju, ili kad koristis tranformaciju mnozenja retka skalarom i dodavanje drugom... tu nije problem mnozenje s 0 (na kraju krajeva to nikako nebi ni utjecalo na sustav) vec dijeljenja s 0, npr. u tvojoj 3. matrici da bi ponistila 3. stupac moras 3. redak mnoziti redom s ) sto najcesce mozes izbjeci da ni ne koristis tu tranformaciju, ili kad koristis tranformaciju mnozenja retka skalarom i dodavanje drugom... tu nije problem mnozenje s 0 (na kraju krajeva to nikako nebi ni utjecalo na sustav) vec dijeljenja s 0, npr. u tvojoj 3. matrici da bi ponistila 3. stupac moras 3. redak mnoziti redom s 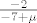 , odnosno , odnosno 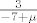 , sto ne smijes iz ocitih razloga ako je , sto ne smijes iz ocitih razloga ako je 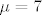 . .
E sad sto se tice razlikovanja slucaja 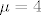 , ovdje nema potrebe za tim, jer zasto nebi mogao slobodni clan biti 0? Problem bi nastao da su svi ostali elementi retka jednaki 0, a slobodni clan razlicit od 0, tad sustav nebi imao rjesenje. , ovdje nema potrebe za tim, jer zasto nebi mogao slobodni clan biti 0? Problem bi nastao da su svi ostali elementi retka jednaki 0, a slobodni clan razlicit od 0, tad sustav nebi imao rjesenje.
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
 Postano: 17:31 pon, 3. 1. 2011 Naslov: Postano: 17:31 pon, 3. 1. 2011 Naslov: |
    |
|
|
[quote="pmli"][quote="Lanek_"]evo potrudila se i sve napisala. xD[/quote]
:karma:
Dobar ti je postupak, samo[b] nema potrebe za slučajem [latex]\mu = 4[/latex].[/b] Moj komentar u vezi zvanja [latex]\mu[/latex] parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš [latex]\mu = 4[/latex] u prvi slučaj, dobit ćeš isto što i u trećem. :)
[/quote]
joj da, imas pravo :)
hvala ti puno na pomoci, sad mi je jasnije sve :lol:
i jos nes, jel bi bilo krivo kod rjesenja napisat ovak:
[latex]\begin{pmatrix}
1-\mu-3t\\
-1+\mu+t\\
1\\
t \\
\end{pmatrix}
=
\mu\begin{pmatrix}
-1\\
1\\
0\\
0
\end{pmatrix}
+
t\begin{pmatrix}
-3\\
1\\
0\\
1
\end{pmatrix}
+
\begin{pmatrix}
1\\
-1\\
1\\
0
\end{pmatrix}
[/latex]
ili nema potreba "vaditi" [latex]\mu[/latex] van?
jer ja sam tak zapisivala rjesenja, pa sam zato govorila da se radi o 2 parametra.
| pmli (napisa): | | Lanek_ (napisa): | | evo potrudila se i sve napisala. xD |

Dobar ti je postupak, samo nema potrebe za slučajem 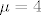 . Moj komentar u vezi zvanja . Moj komentar u vezi zvanja 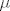 parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš parametrom "rješenja sustava" i dalje stoji. Primjeti da, ako uvrstiš 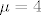 u prvi slučaj, dobit ćeš isto što i u trećem. u prvi slučaj, dobit ćeš isto što i u trećem. 
|
joj da, imas pravo 
hvala ti puno na pomoci, sad mi je jasnije sve 
i jos nes, jel bi bilo krivo kod rjesenja napisat ovak:
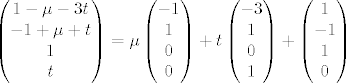
ili nema potreba "vaditi" 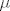 van? van?
jer ja sam tak zapisivala rjesenja, pa sam zato govorila da se radi o 2 parametra.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:04 pon, 3. 1. 2011 Naslov: Postano: 18:04 pon, 3. 1. 2011 Naslov: |
    |
|
|
[quote="Lanek_"]i jos nes, jel bi bilo krivo kod rjesenja napisat ovak:
[latex]\begin{pmatrix}
1-\mu-3t\\
-1+\mu+t\\
1\\
t \\
\end{pmatrix}
=
\mu\begin{pmatrix}
-1\\
1\\
0\\
0
\end{pmatrix}
+
t\begin{pmatrix}
-3\\
1\\
0\\
1
\end{pmatrix}
+
\begin{pmatrix}
1\\
-1\\
1\\
0
\end{pmatrix}
[/latex]
ili nema potreba "vaditi" [latex]\mu[/latex] van?
jer ja sam tak zapisivala rjesenja, pa sam zato govorila da se radi o 2 parametra.[/quote]
Pa, strogo rečeno, nema tu ništa krivog. Ta jednakost doista vrijedi za sve [latex]\mu[/latex] (na koje se odnosi taj slučaj) i [latex]t[/latex]. Ipak, poanta je da se odmah vidi partikularno i homogeno rješenje i kaže što su parametri. Dakle, ovako bi bilo najprimjerenije zapisati rješenje:
[latex]\begin{pmatrix}
1-\mu \\
-1+\mu \\
1 \\
0 \\
\end{pmatrix} + t \begin{pmatrix}
-3 \\
1 \\
0 \\
1 \\
\end{pmatrix}, \ t \in \mathbb{R}[/latex].
(Uoči "ukras" [latex]t \in \mathbb{R}[/latex] :))
| Lanek_ (napisa): | i jos nes, jel bi bilo krivo kod rjesenja napisat ovak:
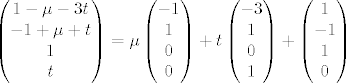
ili nema potreba "vaditi" 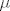 van? van?
jer ja sam tak zapisivala rjesenja, pa sam zato govorila da se radi o 2 parametra. |
Pa, strogo rečeno, nema tu ništa krivog. Ta jednakost doista vrijedi za sve 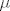 (na koje se odnosi taj slučaj) i (na koje se odnosi taj slučaj) i  . Ipak, poanta je da se odmah vidi partikularno i homogeno rješenje i kaže što su parametri. Dakle, ovako bi bilo najprimjerenije zapisati rješenje: . Ipak, poanta je da se odmah vidi partikularno i homogeno rješenje i kaže što su parametri. Dakle, ovako bi bilo najprimjerenije zapisati rješenje:
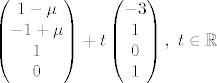 . .
(Uoči "ukras"   ) )
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:03 uto, 1. 2. 2011 Naslov: Postano: 12:03 uto, 1. 2. 2011 Naslov: |
    |
|
|
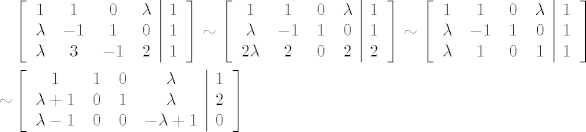
[latex]$\begin{align} & \left[ \begin{array}{cccc|c}
1 & 1 & 0 & \lambda & 1 \\
\lambda & -1 & 1 & 0 & 1 \\
\lambda & 3 & -1 & 2 & 1
\end{array} \right] \sim \left[ \begin{array}{cccc|c}
1 & 1 & 0 & \lambda & 1 \\
\lambda & -1 & 1 & 0 & 1 \\
2 \lambda & 2 & 0 & 2 & 2
\end{array} \right] \sim \left[ \begin{array}{cccc|c}
1 & 1 & 0 & \lambda & 1 \\
\lambda & -1 & 1 & 0 & 1 \\
\lambda & 1 & 0 & 1 & 1
\end{array} \right] \\ \sim & \left[ \begin{array}{cccc|c}
1 & 1 & 0 & \lambda & 1 \\
\lambda + 1 & 0 & 1 & \lambda & 2 \\
\lambda - 1 & 0 & 0 & -\lambda + 1 & 0
\end{array} \right]
\end{align}$[/latex]
1° [latex]\lambda = 1[/latex]
[latex]\left[ \begin{array}{cccc|c}
1 & 1 & 0 & 1 & 1 \\
2 & 0 & 1 & 1 & 2
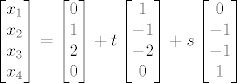
\end{array} \right][/latex], [latex]\begin{bmatrix}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{bmatrix} = \begin{bmatrix}
0 \\ 1 \\ 2 \\ 0
\end{bmatrix} + t \begin{bmatrix}
1 \\ -1 \\ -2 \\ 0
\end{bmatrix} + s \begin{bmatrix}
0 \\ -1 \\ -1 \\ 1
\end{bmatrix}[/latex], [latex]t, s \in \mathbb{R}[/latex]
2° [latex]\lambda \neq 1[/latex]
[latex]\left[\begin{array}{cccc|c}
1 & 1 & 0 & \lambda & 1 \\
\lambda + 1 & 0 & 1 & \lambda & 2 \\
1 & 0 & 0 & -1 & 0
\end{array}\right] \sim \left[\begin{array}{cccc|c}
0 & 1 & 0 & \lambda + 1 & 1 \\
0 & 0 & 1 & 2 \lambda + 1 & 2 \\
1 & 0 & 0 & -1 & 0
\end{array}\right][/latex], [latex]\begin{bmatrix}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{bmatrix} = \begin{bmatrix}
0 \\ 1 \\ 2 \\ 0
\end{bmatrix} + t \begin{bmatrix}
1 \\ -\lambda - 1 \\ -2\lambda - 1 \\ 1
\end{bmatrix}[/latex], [latex]t \in \mathbb{R}[/latex]
1° 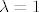
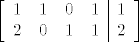 , ,  , , 
2° 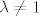
 , , 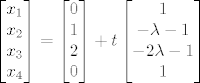 , , 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 16:44 uto, 1. 2. 2011 Naslov: Postano: 16:44 uto, 1. 2. 2011 Naslov: |
    |
|
|
[quote="pmli"]Ne znam o kojim recima govoriš, ali možeš zaključiti da nema rješenja samo ako su lijevo nule, a desno nešto različito od nule, npr. 0 0 0 0 | 3. :)[/quote]
U trecem koraku reduciranja matrice, ako drugi redak pomnozis s -1 i dodas ga trecem, rjesiti cemo se lambde i dobiti cemo da sustav nema rjesenja.
| pmli (napisa): | Ne znam o kojim recima govoriš, ali možeš zaključiti da nema rješenja samo ako su lijevo nule, a desno nešto različito od nule, npr. 0 0 0 0 | 3.  |
U trecem koraku reduciranja matrice, ako drugi redak pomnozis s -1 i dodas ga trecem, rjesiti cemo se lambde i dobiti cemo da sustav nema rjesenja.
|
|
| [Vrh] |
|
|

















