| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:04 sri, 9. 12. 2009 Naslov: Postano: 17:04 sri, 9. 12. 2009 Naslov: |
    |
|
|
Budući da su postojale četiri grupe, vjerojatno bi u postu imalo smisla u tom kontekstu spomenuti neki prirodni broj u intervalu [1,4]. :)
Anyway, ako se radi o prvoj grupi (a bila bi dosta velika slučajnost da se ne radi :lol:), onda mislim da ti je točno. :)
[size=9](Inače, zanimljivo je kako to koliko još vremena ima do kolokvija, neovisno o pojedincu, nije pretjerano neprekidna funkcija... u trenu (obično negdje tjedan dana prije kolokvija) promijeni vrijednost iz "maaa daaaaleko 8) " u "ufff... bliiizu :twisted:".)[/size]
Budući da su postojale četiri grupe, vjerojatno bi u postu imalo smisla u tom kontekstu spomenuti neki prirodni broj u intervalu [1,4]. 
Anyway, ako se radi o prvoj grupi (a bila bi dosta velika slučajnost da se ne radi  ), onda mislim da ti je točno. ), onda mislim da ti je točno. 
(Inače, zanimljivo je kako to koliko još vremena ima do kolokvija, neovisno o pojedincu, nije pretjerano neprekidna funkcija... u trenu (obično negdje tjedan dana prije kolokvija) promijeni vrijednost iz "maaa daaaaleko  " u "ufff... bliiizu " u "ufff... bliiizu  ".) ".)
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:05 sri, 9. 12. 2009 Naslov: Postano: 21:05 sri, 9. 12. 2009 Naslov: |
    |
|
|
Dakle, u vezi tih zadataka (1. i 3. grupa) smo se kolega i ja prošle godine dosta mučili, znam da nam je jedan od njih posebno zadavao muke, ali ne znam koji od ta dva. Valjda je ipak veći problem bio u 3. grupi (ako se ne varam, pojavila se i informacija da zadatak sadrži tipfeler ili tako nešto, pa da zapravo nije bio tako ni zamišljen... možda netko zna više), jer mislim da sam ovaj uspio riješiti.
Kažem, zadatak je dosta težak (osim ako ne postoji neki trik), rješenje bi moglo ići otprilike ovako (nisam pretjerano precizan u ovom pisanju, ali mislim da sve napisano može biti i rigoroznije dokazano):
Nazivnik se da faktorizirati, on iznosi [latex](5-2n)(m+1)[/latex]. Prvo odvojeno promatramo slučajeve [latex]n=1[/latex] i [latex]n=2[/latex].
Neka je [latex]n=1[/latex]. Tada imamo razlomke oblika [latex]\frac{9m+8}{3m+3}=3-\frac{1}{3m+3}.[/latex] Tu je očito supremum [latex]3[/latex], a infimum [latex]\frac{17}{6}[/latex].
Neka je sada [latex]n=2[/latex]. U tom slučaju imamo razlomke oblika [latex]\frac{6m+9}{m+1}=6+\frac{3}{m+1}[/latex]. Tada je supremum [latex]\frac{15}{2}[/latex], a infimum [latex]6[/latex].
I sad idemo na glavni slučaj: [latex]n>2[/latex]. Tu je nazivnik negativan, tj. imamo razlomke oblika [latex]-\frac{12m+n-3mn+7}{(m+1)(2n-5)}[/latex]. Fiksirajmo [latex]n[/latex]. Želimo pokazati da je sad [latex]-\frac{12m+n-3mn+7}{(m+1)(2n-5)}[/latex] rastuće kako se [latex]m[/latex] povećava.
To znači da želimo pokazati kako je [latex]\frac{12m+n-3mn+7}{m+1}[/latex] padajući niz (podsjećam, s fiksnim [latex]n[/latex]). No, [latex]\frac{12m+n-3mn+7}{m+1})=\frac{12m-3mn+12-3n+4n-5}{m+1}=12-3n+\frac{4n-5}{m+1}[/latex]. Kako je [latex]n[/latex] konstantan, a [latex]4n-5[/latex] pozitivan, onda [latex]\frac{4n-5}{m+1}[/latex] pada, pa smo tvrdnju dokazali.
Dakle, u svakom od ovih slučajeva infimum se postiže za [latex]m=1[/latex], a supremum je limes za [latex]m\rightarrow +\infty[/latex] (uz fiksirani [latex]n[/latex]).
Pogledajmo koliki su ti infimumi i supremumi. Za [latex]m=1[/latex] imamo da je razlomak za svaki [latex]n[/latex] jednak [latex]-\frac{19-2n}{2(2n-5)}=-\frac{1}{2}(-1+\frac{14}{2n-5})=\frac{1}{2}-\frac{7}{2n-5}[/latex]. Nas zanima samo najmanji od tih infimuma, a on se postiže za [latex]n=3[/latex] (uzeli smo [latex]n>2[/latex]) i iznosi [latex]\frac{-13}{2}[/latex].
Još nas zanima supremum. Dakle, fiksiramo [latex]n[/latex] i pokazali smo da se supremum ne postiže, tj. da ga dobivamo na limesu za [latex]m\rightarrow +\infty[/latex]. Stoga, zanima nas [latex]-\frac{12m+n-3mn+7}{(m+1)(2n-5)}=-\frac{1}{2n-5}\cdot\frac{((12-3n)m+n+7}{m+1}\rightarrow -\frac{12-3n}{2n-5}=\frac{3n-12}{2n-5}[/latex]. Lako dobivamo da to iznosi [latex]\frac{3}{2}-\frac{9}{2(2n-5)}[/latex]. Zanima nas najveći od tih supremuma, a on se također tek "postiže u beskonačnosti" i iznosi [latex]\frac{3}{2}[/latex].
Sad smo došli do kraja. Kad pogledamo sve infimume i supremume, "ukupni infimum" je najmanji od njih, a to je [latex]\frac{-13}{2}[/latex] (postiže se za [latex]m=1[/latex], [latex]n=3[/latex]), a "ukupni supremum" najveći od svih supremuma, a to je [latex]\frac{15}{2}[/latex] (postiže se za [latex]m=1[/latex], [latex]n=2[/latex]).
Evo, to bi bilo to, nadam se da negdje nisam pogriješio, makar su šanse za to (da nisam pogriješio, ne da jesam :D) sasvim minimalne. :) Možda smo mogli i malo "varati" (npr. naći infimume i supremume, a zatim dokazati da su sve ostale vrijednosti između njih), ali ovo je napravljeno baš onako "školski" i ne vidi se pretjerano da sam koristio kalkulator. :)
Valjda onda 3. grupa ima taj "nerješiv"... :?
Dakle, u vezi tih zadataka (1. i 3. grupa) smo se kolega i ja prošle godine dosta mučili, znam da nam je jedan od njih posebno zadavao muke, ali ne znam koji od ta dva. Valjda je ipak veći problem bio u 3. grupi (ako se ne varam, pojavila se i informacija da zadatak sadrži tipfeler ili tako nešto, pa da zapravo nije bio tako ni zamišljen... možda netko zna više), jer mislim da sam ovaj uspio riješiti.
Kažem, zadatak je dosta težak (osim ako ne postoji neki trik), rješenje bi moglo ići otprilike ovako (nisam pretjerano precizan u ovom pisanju, ali mislim da sve napisano može biti i rigoroznije dokazano):
Nazivnik se da faktorizirati, on iznosi 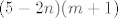 . Prvo odvojeno promatramo slučajeve . Prvo odvojeno promatramo slučajeve 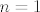 i i  . .
Neka je 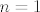 . Tada imamo razlomke oblika . Tada imamo razlomke oblika 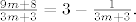 Tu je očito supremum Tu je očito supremum 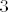 , a infimum , a infimum 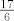 . .
Neka je sada  . U tom slučaju imamo razlomke oblika . U tom slučaju imamo razlomke oblika 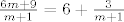 . Tada je supremum . Tada je supremum 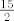 , a infimum , a infimum  . .
I sad idemo na glavni slučaj: 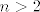 . Tu je nazivnik negativan, tj. imamo razlomke oblika . Tu je nazivnik negativan, tj. imamo razlomke oblika 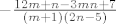 . Fiksirajmo . Fiksirajmo  . Želimo pokazati da je sad . Želimo pokazati da je sad 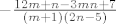 rastuće kako se rastuće kako se  povećava. povećava.
To znači da želimo pokazati kako je 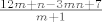 padajući niz (podsjećam, s fiksnim padajući niz (podsjećam, s fiksnim  ). No, ). No, 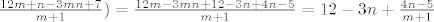 . Kako je . Kako je  konstantan, a konstantan, a 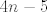 pozitivan, onda pozitivan, onda 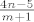 pada, pa smo tvrdnju dokazali. pada, pa smo tvrdnju dokazali.
Dakle, u svakom od ovih slučajeva infimum se postiže za 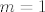 , a supremum je limes za , a supremum je limes za 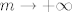 (uz fiksirani (uz fiksirani  ). ).
Pogledajmo koliki su ti infimumi i supremumi. Za 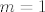 imamo da je razlomak za svaki imamo da je razlomak za svaki  jednak jednak 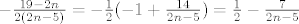 . Nas zanima samo najmanji od tih infimuma, a on se postiže za . Nas zanima samo najmanji od tih infimuma, a on se postiže za 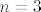 (uzeli smo (uzeli smo 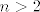 ) i iznosi ) i iznosi 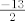 . .
Još nas zanima supremum. Dakle, fiksiramo  i pokazali smo da se supremum ne postiže, tj. da ga dobivamo na limesu za i pokazali smo da se supremum ne postiže, tj. da ga dobivamo na limesu za 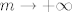 . Stoga, zanima nas . Stoga, zanima nas 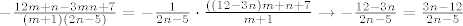 . Lako dobivamo da to iznosi . Lako dobivamo da to iznosi 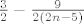 . Zanima nas najveći od tih supremuma, a on se također tek "postiže u beskonačnosti" i iznosi . Zanima nas najveći od tih supremuma, a on se također tek "postiže u beskonačnosti" i iznosi 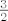 . .
Sad smo došli do kraja. Kad pogledamo sve infimume i supremume, "ukupni infimum" je najmanji od njih, a to je 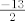 (postiže se za (postiže se za 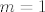 , , 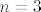 ), a "ukupni supremum" najveći od svih supremuma, a to je ), a "ukupni supremum" najveći od svih supremuma, a to je 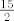 (postiže se za (postiže se za 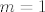 , ,  ). ).
Evo, to bi bilo to, nadam se da negdje nisam pogriješio, makar su šanse za to (da nisam pogriješio, ne da jesam  ) sasvim minimalne. ) sasvim minimalne.  Možda smo mogli i malo "varati" (npr. naći infimume i supremume, a zatim dokazati da su sve ostale vrijednosti između njih), ali ovo je napravljeno baš onako "školski" i ne vidi se pretjerano da sam koristio kalkulator. Možda smo mogli i malo "varati" (npr. naći infimume i supremume, a zatim dokazati da su sve ostale vrijednosti između njih), ali ovo je napravljeno baš onako "školski" i ne vidi se pretjerano da sam koristio kalkulator. 
Valjda onda 3. grupa ima taj "nerješiv"... 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 17:51 uto, 15. 12. 2009 Naslov: Postano: 17:51 uto, 15. 12. 2009 Naslov: |
    |
|
|
[quote="vuja"]imam jedno pitanje i ne otvara mi se nova tema... da li postoji kakva knjiga/skripta/udžbenik/bilo šta, gdje bi se mogli pronaći dokazi teorema koje dokazujemo na predavanjima i vježbama. po mogućnosti pojašnjeni. hvala unaprijed :D[/quote]
skripta, bilježnica, konzultacije, demonstrature, stariji kolege, a vjerojatno da nečeg ima i na Google-u
| vuja (napisa): | imam jedno pitanje i ne otvara mi se nova tema... da li postoji kakva knjiga/skripta/udžbenik/bilo šta, gdje bi se mogli pronaći dokazi teorema koje dokazujemo na predavanjima i vježbama. po mogućnosti pojašnjeni. hvala unaprijed  |
skripta, bilježnica, konzultacije, demonstrature, stariji kolege, a vjerojatno da nečeg ima i na Google-u
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:46 pon, 28. 12. 2009 Naslov: Postano: 14:46 pon, 28. 12. 2009 Naslov: |
    |
|
|
Ako sam ja dobro shvatio što ti pitaš (a u to nisam baš uvjeren :lol:)... :)
Dobro, nebitno je što se tiče ostatka tvojeg pitanja, ali [latex]\cos (m\pi)[/latex] nije jednako [latex]0[/latex] niti za jedan [latex]m\in\mathbb{Z}[/latex] - uvijek je ili [latex]1[/latex] (ako je [latex]m[/latex] paran) ili [latex]-1[/latex] (ako je [latex]m[/latex] neparan). Stoga su ta dva slučaja jedini koji nas interesiraju. Naime, kao što si rekla, da kosinus bude [latex]0[/latex] trebali bismo imati [latex]\displaystyle m=k\pm \frac{1}{2}[/latex] za neki [latex]k\in\mathbb{Z}[/latex], što je očito nemoguće, budući da je [latex]m[/latex] cijeli broj.
A dalje, ako te dobro shvaćam, ti pitaš koja je razlika između skupa [latex]\displaystyle \{k+\frac{1}{2}: k\in\mathbb{Z}\}[/latex], kojeg si dobila jednim računom, i skupa [latex]\displaystyle \{k-\frac{1}{2}: k\in\mathbb{Z}\}[/latex], kojeg si dobila drugim računom i što je onda točno od tog dvoje itd. Odgovor je jednostavan - ta dva skupa su, makar izgledaju različito, potpuno isti, pa nije ni čudno što si ih dobila.
Dakako, može se dati i formalnije objašnjenje (to su skupovi svih brojeva koji su od prethodnog, odnosno sljedećeg, cijelog broja udaljeni za [latex]\displaystyle \frac{1}{2}[/latex], ali mislim da će ti ovo biti sasvim razumno: [latex]\displaystyle \{k+\frac{1}{2}: k\in\mathbb{Z}\}=\{\ldots, -2+\frac{1}{2}, -1+\frac{1}{2}, 0+\frac{1}{2}, 1+\frac{1}{2}, 2+\frac{1}{2}, \ldots\}=\{\ldots, -\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \ldots\}[/latex]. S druge strane, [latex]\displaystyle \{k-\frac{1}{2}: k\in\mathbb{Z}\}=\{\ldots, -2-\frac{1}{2}, -1-\frac{1}{2}, 0-\frac{1}{2}, 1-\frac{1}{2}, 2-\frac{1}{2}, \ldots\}=\{\ldots, -\frac{5}{2}, -\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \ldots\}[/latex]. Stoga, vidiš da se zapravo radi o istim skupovima.
Također, primijeti da je [latex]\{2k+1: k\in\mathbb{Z}\}[/latex] skup svih neparnih brojeva, isto kao i [latex]\{2k-1: k\in\mathbb{Z}\}[/latex] (to opet možeš zornije vidjeti tako da napišeš zaredom nekoliko članova ta dva skupa), pa su i ova dva skupa ista, pa nemaš grešku u rješavanju :).
Ako sam ja dobro shvatio što ti pitaš (a u to nisam baš uvjeren  )... )... 
Dobro, nebitno je što se tiče ostatka tvojeg pitanja, ali 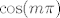 nije jednako nije jednako  niti za jedan niti za jedan 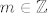 - uvijek je ili - uvijek je ili  (ako je (ako je  paran) ili paran) ili  (ako je (ako je  neparan). Stoga su ta dva slučaja jedini koji nas interesiraju. Naime, kao što si rekla, da kosinus bude neparan). Stoga su ta dva slučaja jedini koji nas interesiraju. Naime, kao što si rekla, da kosinus bude  trebali bismo imati trebali bismo imati 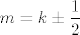 za neki za neki 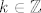 , što je očito nemoguće, budući da je , što je očito nemoguće, budući da je  cijeli broj. cijeli broj.
A dalje, ako te dobro shvaćam, ti pitaš koja je razlika između skupa 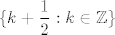 , kojeg si dobila jednim računom, i skupa , kojeg si dobila jednim računom, i skupa 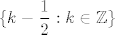 , kojeg si dobila drugim računom i što je onda točno od tog dvoje itd. Odgovor je jednostavan - ta dva skupa su, makar izgledaju različito, potpuno isti, pa nije ni čudno što si ih dobila. , kojeg si dobila drugim računom i što je onda točno od tog dvoje itd. Odgovor je jednostavan - ta dva skupa su, makar izgledaju različito, potpuno isti, pa nije ni čudno što si ih dobila.
Dakako, može se dati i formalnije objašnjenje (to su skupovi svih brojeva koji su od prethodnog, odnosno sljedećeg, cijelog broja udaljeni za  , ali mislim da će ti ovo biti sasvim razumno: , ali mislim da će ti ovo biti sasvim razumno: 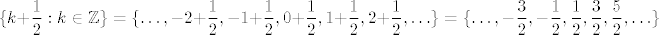 . S druge strane, . S druge strane, 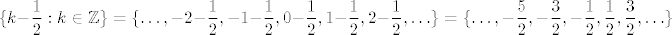 . Stoga, vidiš da se zapravo radi o istim skupovima. . Stoga, vidiš da se zapravo radi o istim skupovima.
Također, primijeti da je 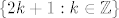 skup svih neparnih brojeva, isto kao i skup svih neparnih brojeva, isto kao i 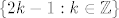 (to opet možeš zornije vidjeti tako da napišeš zaredom nekoliko članova ta dva skupa), pa su i ova dva skupa ista, pa nemaš grešku u rješavanju (to opet možeš zornije vidjeti tako da napišeš zaredom nekoliko članova ta dva skupa), pa su i ova dva skupa ista, pa nemaš grešku u rješavanju  . .
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:26 pon, 28. 12. 2009 Naslov: Postano: 15:26 pon, 28. 12. 2009 Naslov: |
    |
|
|
Daklem, poanta je racionalizirati nazivnik, kao i u manje-više svim takvim zadacima s korijenima. Kad to tri bespomoćne djevojke naprave, garantirano su gotove :D. Uglavnom, [latex]\displaystyle \lim_{x\rightarrow 0}\frac{\sqrt{x+9}-x-3}{\sqrt{x+9}-3}=\lim_{x\rightarrow 0}\frac{(\sqrt{x+9}-x-3)(\sqrt{x+9}+3)}{(\sqrt{x+9}-3)(\sqrt{x+9}+3)}=\lim_{x\rightarrow 0}\frac{x-x(\sqrt{x+9}+3)}{x}[/latex]. Rezultat je sada očito [latex]\displaystyle \frac{1-(\sqrt{0+9}+3)}{1}=-5[/latex].
Uglavnom, ovaj zadatak je bio zbilja lagan i ima zapravo samo jednu ideju, koja se ionako na vježbama i demonstraturama spominje do iznemoglosti, a to je riješiti se korijena u nazivniku (možda se poslije ne vidi odmah da se može izlučiti [latex]x[/latex] iz brojnika, ali i to se dobije, u najgorem slučaju pomnoživši svaki član sa svakim). :D
Daklem, poanta je racionalizirati nazivnik, kao i u manje-više svim takvim zadacima s korijenima. Kad to tri bespomoćne djevojke naprave, garantirano su gotove  . Uglavnom, . Uglavnom, 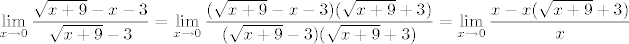 . Rezultat je sada očito . Rezultat je sada očito 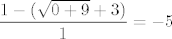 . .
Uglavnom, ovaj zadatak je bio zbilja lagan i ima zapravo samo jednu ideju, koja se ionako na vježbama i demonstraturama spominje do iznemoglosti, a to je riješiti se korijena u nazivniku (možda se poslije ne vidi odmah da se može izlučiti  iz brojnika, ali i to se dobije, u najgorem slučaju pomnoživši svaki član sa svakim). iz brojnika, ali i to se dobije, u najgorem slučaju pomnoživši svaki član sa svakim). 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
|









