| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 10:19 pet, 24. 4. 2009 Naslov: Postano: 10:19 pet, 24. 4. 2009 Naslov: |
    |
|
|
za prvi nisam siguran... taj i mene zanima...
al drugi...vektorski...
izrazis PQ, QR, PR preko AB, BC, AC...to ti nije tesko jer znas one omjere...
e sad, uzmes neku tocku T kao teziste trokuta ABC... i sad racunas PT+RT+QT... i to ti mora biti =0...
zapravo, nece ti biti 0, nego ces dobiti neki uvjet vezan za trokut ABC... al on ce ti biti u redu... (najvjerojatnije ce biti nesto s tezistem)... ovo je onak okvirno, kaj ja mislim da ce ispast, sad jos to treba izracunat... :)
za prvi nisam siguran... taj i mene zanima...
al drugi...vektorski...
izrazis PQ, QR, PR preko AB, BC, AC...to ti nije tesko jer znas one omjere...
e sad, uzmes neku tocku T kao teziste trokuta ABC... i sad racunas PT+RT+QT... i to ti mora biti =0...
zapravo, nece ti biti 0, nego ces dobiti neki uvjet vezan za trokut ABC... al on ce ti biti u redu... (najvjerojatnije ce biti nesto s tezistem)... ovo je onak okvirno, kaj ja mislim da ce ispast, sad jos to treba izracunat... 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:40 pet, 24. 4. 2009 Naslov: Postano: 13:40 pet, 24. 4. 2009 Naslov: |
    |
|
|
Za prvi zadatak, pokažimo najprije da je pravac [latex]s[/latex] koji prolazi točkom [latex]O[/latex] simetrala kuta [latex]\angle{pOq}[/latex] ako i samo ako za svaku točku [latex]X \in s[/latex] vrijedi da je [latex]d\left(X,\,p\right)=d\left(X,\,q\right)[/latex], gdje [latex]d\left(X,\,p\right)[/latex] označava udaljenost između točke [latex]X[/latex] i pravca [latex]p[/latex].
Pretpostavimo najprije da je pravac [latex]s[/latex] simetrala kuta [latex]\angle{pOq}[/latex], sada uzmimo proizvoljnu točku [latex]X\in s\setminus{\left\{O\right\}}[/latex], neka je [latex]A[/latex] točka presjeka pravca [latex]p[/latex] s okomicom iz [latex]X[/latex] na [latex]p[/latex], te točka [latex]B[/latex] analogno definirana na [latex]q[/latex]. Trokuti [latex]OAX[/latex] i [latex]OBX[/latex] su pravokutni, te imaju jedan šiljasti kut jednak [latex]\left(\measuredangle{XOA}=\measuredangle{XOB}\right)[/latex], stoga imaju sve kuteve jednaka, pa su slični, no, imaju i zajedničku stranicu [latex]\overline{OX}[/latex] pa su sukladni, iz ovoga direktno slijedi da je [latex]\left|XA\right|=\left|XB\right|[/latex].
Sada, neka je [latex]s[/latex] pravac povučen točkom [latex]O[/latex] takav da za svaku točku [latex]X \in s[/latex] vrijedi da je [latex]d\left(X,\,p\right)=d\left(X,\,q\right)[/latex], uzmimo proizvoljnu točku [latex]X \in s \setminus{\left\{O\right\}}[/latex]. Neka su točke [latex]A[/latex] i [latex]B[/latex] definirane kao maloprije na pravcima [latex]p[/latex] i [latex]q[/latex]. Vrijedi [latex]\left|XA\right|=\left|XB\right|[/latex], [latex]\measuredangle{XAO}=\frac{\pi}{2}=\measuredangle{XBO}[/latex], te [latex]\left|XO\right|=\left|XO\right|[/latex] i [latex]\left|XO\right|>\left|XA\right|[/latex], [latex]\left|XO\right|>\left|XB\right|[/latex] (hipotenuza pravokutnog trokuta je veća od kateta). Stoga su trokuti [latex]AXO[/latex] i [latex]BXO[/latex] sukladni, pa je [latex]\measuredangle{XOA}=\measuredangle{XOB}[/latex].
Neka je sada [latex]ABC[/latex] proizvoljan trokut, te neka su [latex]s_A[/latex], [latex]s_B[/latex], [latex]s_C[/latex] redom simetrale kuteva pri vrhovima [latex]A[/latex], [latex]B[/latex], [latex]C[/latex]. Neka je [latex]T:=s_A \cap s_B[/latex]. Sada je jasno da ako pokažemo da je [latex]T \in s_C[/latex] da smo gotovi. Kako je [latex]T \in s_A[/latex] vrijedi [latex]d\left(T,\,AB\right)=d\left(T,\,AC\right)[/latex], a kako je i [latex]T \in s_B[/latex] vrijedi da je [latex]d\left(T,\,BA\right)=d\left(T,\,BC\right)[/latex]. Zato je [latex]d\left(T,\,CA\right)=d\left(T,\,CB\right)[/latex], odnosno [latex]T \in s_C[/latex].
Za drugi zadatak najprije pokažimo da je točka [latex]T[/latex] težište trokuta [latex]ABC[/latex] ako i samo ako je [latex]\overrightarrow{AT}+\overrightarrow{BT}+\overrightarrow{CT}=\overrightarrow{0}[/latex].
Neka je [latex]T[/latex] težište trokuta [latex]ABC[/latex]. Točka [latex]P[/latex] neka je polovište stranice [latex]\overline{BC}[/latex], a točka [latex]D[/latex] takva da je četverokut [latex]BDCT[/latex] paralelogram. Sada je
[latex]\overrightarrow{AT}=2\overrightarrow{TP}=\overrightarrow{TD}=\overrightarrow{TB}+\overrightarrow{BD}=\overrightarrow{TB}+\overrightarrow{TC}=-\overrightarrow{BT}-\overrightarrow{CT} \Longrightarrow \overrightarrow{AT}+\overrightarrow{BT}+\overrightarrow{CT}=\overrightarrow{0}[/latex].
Dalje, neka je [latex]T[/latex] točka ravnine trokuta [latex]ABC[/latex] takva da vrijedi da je [latex]\overrightarrow{AT}+\overrightarrow{BT}+\overrightarrow{CT}=\overrightarrow{0}[/latex]. Odmah je jasno da točka [latex]T[/latex] mora biti u unutrašnjosti trokuta [latex]ABC[/latex]. Neka je točka [latex]D[/latex] takva da je četverokut [latex]ADBT[/latex] paralelogram. Iz uvjeta vrijedi da je [latex]\overrightarrow{CT}=-\overrightarrow{AT}-\overrightarrow{BT}=\overrightarrow{TA}+\overrightarrow{TB}=\overrightarrow{TA}+\overrightarrow{AD}=\overrightarrow{TD}[/latex]. Dakle, pravci [latex]CT[/latex] i [latex]TD[/latex] su identični, a kako se dijagonale paralelograma raspolovljavaju, jasno je da pravac [latex]CT[/latex] prolazi polovištem stranice [latex]\overline{AB}[/latex]. Analogno pokazujemo da pravci [latex]AT[/latex] i [latex]BT[/latex] raspolovljavaju stranice [latex]\overline{BC}[/latex] i [latex]\overline{CA}[/latex]. Dakle, točka [latex]T[/latex] je težište trokuta [latex]ABC[/latex].
Bez smanjenja općenitosti možemo pretpostaviti da je [latex]\left|AP\right| \leq \frac{1}{2}\left|AB\right|[/latex]. Prema uvjetu zadatka tada vrijedi da je [latex]\frac{\left|AP\right|}{\left|PB\right|}=\frac{\left|BQ\right|}{\left|QC\right|}=\frac{\left|CR\right|}{\left|RA\right|}=k[/latex], gdje je [latex]k \in \left<0,\,1\right][/latex]. Neka je [latex]T[/latex] težište trokuta [latex]ABC[/latex], sada je dovoljno pokazati da je [latex]\overrightarrow{PT}+\overrightarrow{QT}+\overrightarrow{RT}=\overrightarrow{0}[/latex].
Vrijedi [latex]\overrightarrow{AP}=k\overrightarrow{PB}=k\left(\overrightarrow{PA}+\overrightarrow{AB}\right)=k\left(\overrightarrow{AB}-\overrightarrow{AP}\right) \Longrightarrow \overrightarrow{AP}=\frac{k}{k+1}\overrightarrow{AB}[/latex].
Neka je [latex]D[/latex] polovište stranice [latex]\overline{AB}[/latex], sada je
[latex]\overrightarrow{PT}=\overrightarrow{PD}+\overrightarrow{DT}=\overrightarrow{PA}+\overrightarrow{AD}-\overrightarrow{TD}=-\frac{k}{k+1}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CT}=\frac{1-k}{2\left(k+1\right)}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CT}[/latex].
Analogno nalazimo da je [latex]\overrightarrow{QT}=\frac{1-k}{2\left(k+1\right)}\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AT}[/latex], te [latex]\overrightarrow{RT}=\frac{1-k}{2\left(k+1\right)}\overrightarrow{CA}-\frac{1}{2}\overrightarrow{BT}[/latex].
Konačno je
[latex]\overrightarrow{PT}+\overrightarrow{QT}+\overrightarrow{RT}=\frac{1-k}{2\left(k+1\right)}\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\right)-\frac{1}{2}\left(\overrightarrow{CT}+\overrightarrow{AT}+\overrightarrow{BT}\right)=[/latex]
[latex]=\frac{1-k}{2\left(k+1\right)}\overrightarrow{AA}-\frac{1}{2}\overrightarrow{0}=\overrightarrow{0}[/latex].
Za prvi zadatak, pokažimo najprije da je pravac  koji prolazi točkom koji prolazi točkom 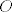 simetrala kuta simetrala kuta 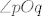 ako i samo ako za svaku točku ako i samo ako za svaku točku  vrijedi da je vrijedi da je 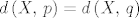 , gdje , gdje 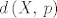 označava udaljenost između točke označava udaljenost između točke  i pravca i pravca  . .
Pretpostavimo najprije da je pravac  simetrala kuta simetrala kuta 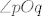 , sada uzmimo proizvoljnu točku , sada uzmimo proizvoljnu točku 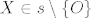 , neka je , neka je  točka presjeka pravca točka presjeka pravca  s okomicom iz s okomicom iz  na na  , te točka , te točka  analogno definirana na analogno definirana na  . Trokuti . Trokuti 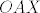 i i 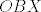 su pravokutni, te imaju jedan šiljasti kut jednak su pravokutni, te imaju jedan šiljasti kut jednak 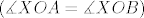 , stoga imaju sve kuteve jednaka, pa su slični, no, imaju i zajedničku stranicu , stoga imaju sve kuteve jednaka, pa su slični, no, imaju i zajedničku stranicu 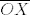 pa su sukladni, iz ovoga direktno slijedi da je pa su sukladni, iz ovoga direktno slijedi da je 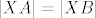 . .
Sada, neka je  pravac povučen točkom pravac povučen točkom 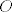 takav da za svaku točku takav da za svaku točku  vrijedi da je vrijedi da je 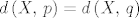 , uzmimo proizvoljnu točku , uzmimo proizvoljnu točku 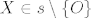 . Neka su točke . Neka su točke  i i  definirane kao maloprije na pravcima definirane kao maloprije na pravcima  i i  . Vrijedi . Vrijedi 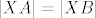 , , 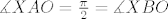 , te , te 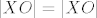 i i 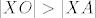 , , 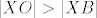 (hipotenuza pravokutnog trokuta je veća od kateta). Stoga su trokuti (hipotenuza pravokutnog trokuta je veća od kateta). Stoga su trokuti 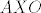 i i 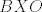 sukladni, pa je sukladni, pa je 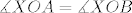 . .
Neka je sada 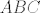 proizvoljan trokut, te neka su proizvoljan trokut, te neka su 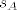 , , 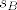 , , 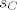 redom simetrale kuteva pri vrhovima redom simetrale kuteva pri vrhovima  , ,  , ,  . Neka je . Neka je 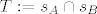 . Sada je jasno da ako pokažemo da je . Sada je jasno da ako pokažemo da je 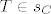 da smo gotovi. Kako je da smo gotovi. Kako je 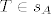 vrijedi vrijedi 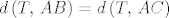 , a kako je i , a kako je i 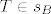 vrijedi da je vrijedi da je 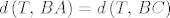 . Zato je . Zato je 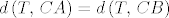 , odnosno , odnosno 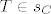 . .
Za drugi zadatak najprije pokažimo da je točka  težište trokuta težište trokuta 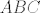 ako i samo ako je ako i samo ako je 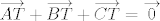 . .
Neka je  težište trokuta težište trokuta 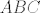 . Točka . Točka  neka je polovište stranice neka je polovište stranice 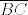 , a točka , a točka 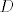 takva da je četverokut takva da je četverokut 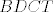 paralelogram. Sada je paralelogram. Sada je
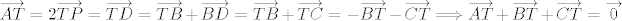 . .
Dalje, neka je  točka ravnine trokuta točka ravnine trokuta 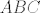 takva da vrijedi da je takva da vrijedi da je 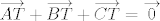 . Odmah je jasno da točka . Odmah je jasno da točka  mora biti u unutrašnjosti trokuta mora biti u unutrašnjosti trokuta 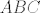 . Neka je točka . Neka je točka 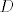 takva da je četverokut takva da je četverokut 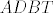 paralelogram. Iz uvjeta vrijedi da je paralelogram. Iz uvjeta vrijedi da je 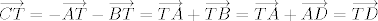 . Dakle, pravci . Dakle, pravci  i i 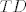 su identični, a kako se dijagonale paralelograma raspolovljavaju, jasno je da pravac su identični, a kako se dijagonale paralelograma raspolovljavaju, jasno je da pravac  prolazi polovištem stranice prolazi polovištem stranice 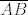 . Analogno pokazujemo da pravci . Analogno pokazujemo da pravci 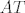 i i 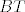 raspolovljavaju stranice raspolovljavaju stranice 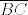 i i 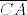 . Dakle, točka . Dakle, točka  je težište trokuta je težište trokuta 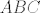 . .
Bez smanjenja općenitosti možemo pretpostaviti da je 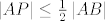 . Prema uvjetu zadatka tada vrijedi da je . Prema uvjetu zadatka tada vrijedi da je 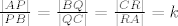 , gdje je , gdje je 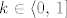 . Neka je . Neka je  težište trokuta težište trokuta 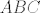 , sada je dovoljno pokazati da je , sada je dovoljno pokazati da je  . .
Vrijedi 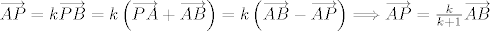 . .
Neka je 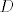 polovište stranice polovište stranice 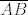 , sada je , sada je
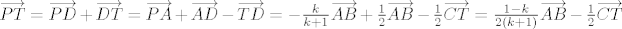 . .
Analogno nalazimo da je 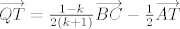 , te , te 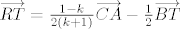 . .
Konačno je
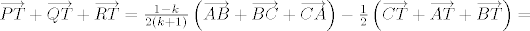
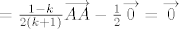 . .
|
|
| [Vrh] |
|
yimpa
Forumaš(ica)
Pridružen/a: 18. 01. 2008. (23:56:37)
Postovi: (26)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
manbearpig
Forumaš(ica)


Pridružen/a: 31. 01. 2009. (19:53:28)
Postovi: (40)16
Spol: 
Lokacija: socijalno nelagodne situacije TAMO SAM
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:46 sub, 25. 4. 2009 Naslov: Postano: 11:46 sub, 25. 4. 2009 Naslov: |
    |
|
|
Dobro si shvatio zadatak i u pravu si, ne vrijedi!
No, tvrdnja vrijedi ukoliko je rječ o TETIVNOM četverokutu.
Naime, neka je četverokut ABCD tetivan (s tim poretkom vrhova), te neka se dijagonale AC i BD sijeku u točki O pod pravim kutem. Neka je dalje točka P polovište stranice CD, ukoliko pokažemo da je pravac OP okomit na stranicu AB dokaz je gotov.
Neka je Q točka presjeka pravaca AB i OP. Vrijedi, <QOB=<DOP. Kako je četverokut ABCD tetivan, vrijedi da je <QBO=<ABD=<ACD=<OCP.
Trokut DOC je pravokutan, pa je |PC|=|PO|, zato je <OCP=POC.
Konačno je <OQB=180°-<QOB-<OBQ=180°-(<DOP+<POC)=180°-90°=90°.
Dobro si shvatio zadatak i u pravu si, ne vrijedi!
No, tvrdnja vrijedi ukoliko je rječ o TETIVNOM četverokutu.
Naime, neka je četverokut ABCD tetivan (s tim poretkom vrhova), te neka se dijagonale AC i BD sijeku u točki O pod pravim kutem. Neka je dalje točka P polovište stranice CD, ukoliko pokažemo da je pravac OP okomit na stranicu AB dokaz je gotov.
Neka je Q točka presjeka pravaca AB i OP. Vrijedi, <QOB=<DOP. Kako je četverokut ABCD tetivan, vrijedi da je <QBO=<ABD=<ACD=<OCP.
Trokut DOC je pravokutan, pa je |PC|=|PO|, zato je <OCP=POC.
Konačno je <OQB=180°-<QOB-<OBQ=180°-(<DOP+<POC)=180°-90°=90°.
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:43 sub, 25. 4. 2009 Naslov: Postano: 12:43 sub, 25. 4. 2009 Naslov: |
    |
|
|
Ne vjerujem da bi se samo skica priznala, ali kad skužiš da ne vrijedi općenito, lako je naći neke konkretne vrijednosti i s njima pokazati da ne vrijedi...
Što se tiče zadatka, neka je dan pravokutan trokut s pravim kutem pri vrhu C. Bez smanjenja općenitosti možemo pretpostaviti da je |AC|>=|BC|. Neka je P polovište hipotenuze AB, a N nožište visine iz vrha C na istu.
Zbog pretspostavke je sada jasno da se točka N nalazi na stranici BP.
Neka je CD (gdje je D na AB) simetrala kuta BCA. Ukoliko pokažemo da je <PCA=<NCB imamo da je <DCP=<DCA-<PCA=<DCB-<NCB=<DCN, pa smo gotovi.
Kako je trokut ABC pravokutan, vrijedi da je |PC|=|PA|, pa je <PCA=<PAC=<BAC=90°-<ABC=90°-<NBC=<NCB.
Ne vjerujem da bi se samo skica priznala, ali kad skužiš da ne vrijedi općenito, lako je naći neke konkretne vrijednosti i s njima pokazati da ne vrijedi...
Što se tiče zadatka, neka je dan pravokutan trokut s pravim kutem pri vrhu C. Bez smanjenja općenitosti možemo pretpostaviti da je |AC|>=|BC|. Neka je P polovište hipotenuze AB, a N nožište visine iz vrha C na istu.
Zbog pretspostavke je sada jasno da se točka N nalazi na stranici BP.
Neka je CD (gdje je D na AB) simetrala kuta BCA. Ukoliko pokažemo da je <PCA=<NCB imamo da je <DCP=<DCA-<PCA=<DCB-<NCB=<DCN, pa smo gotovi.
Kako je trokut ABC pravokutan, vrijedi da je |PC|=|PA|, pa je <PCA=<PAC=<BAC=90°-<ABC=90°-<NBC=<NCB.
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 12:52 sub, 25. 4. 2009 Naslov: Postano: 12:52 sub, 25. 4. 2009 Naslov: |
    |
|
|
[URL=http://www.imagesforme.com/show.php/464138_skica2.jpg][img]http://www.imagesforme.com/out.php/t464138_skica2.jpg[/img][/URL]
ok, dakle...
pokazes da su <FAC i <BAD jednaki <ABC... ovo prvo pokazes preko slicnosti ABC i AFC, a za ovo drugo kaze da je ABD jednakokracan jer je D srediste opisane kruznice pravokutnog trokuta posto se nalazi na polovistu hipotenuze...
e sad kad to dokazes, znas da je <CAE=<EAB=45°
i onda imas
45°=<BAD + <DAE
45°=<CAF + <FAE
posto je <BAD=<CAF, dobivas da je <DAE=<FAE, sto je trebalo i pokazati...

ok, dakle...
pokazes da su <FAC i <BAD jednaki <ABC... ovo prvo pokazes preko slicnosti ABC i AFC, a za ovo drugo kaze da je ABD jednakokracan jer je D srediste opisane kruznice pravokutnog trokuta posto se nalazi na polovistu hipotenuze...
e sad kad to dokazes, znas da je <CAE=<EAB=45°
i onda imas
45°=<BAD + <DAE
45°=<CAF + <FAE
posto je <BAD=<CAF, dobivas da je <DAE=<FAE, sto je trebalo i pokazati...
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
 Postano: 14:47 ned, 26. 4. 2009 Naslov: Postano: 14:47 ned, 26. 4. 2009 Naslov: |
    |
|
|
Evo još jedan zadatak, pokušavam svašta i preko obodnih kuteva i svega al nikako da mi išta dobro ispadne ništa ne dobivam pa pliz helpajte:) zadatak glasi: [b]U kružnicu je upisan trokut, dokaži da nožišta okomica spuštenih iz proizvoljne točke kružnice na njegove stranice leže na jednom pravcu. [/b]Probala sam ovako:trokut ABC, nožište visine na str BC je A' , itd.. Dva nožišta sigurno leže na jednom pravcu,uzmem da su to B' i C', odredim sjecište pravca B'C' i treće stranice trokuta (stranice BC), neka je to A', spojim A' s onom proizvoljnom točkom na kružnici (recimo P) i treba sad dokazat da je pravac PA' visina na BC tj da je to pravi kut??? ugl nisam uspjela ništa dobit...jesam fulala u postavljanju zad? ispričavam se što je ovako opširno.
Evo još jedan zadatak, pokušavam svašta i preko obodnih kuteva i svega al nikako da mi išta dobro ispadne ništa ne dobivam pa pliz helpajte:) zadatak glasi: U kružnicu je upisan trokut, dokaži da nožišta okomica spuštenih iz proizvoljne točke kružnice na njegove stranice leže na jednom pravcu. Probala sam ovako:trokut ABC, nožište visine na str BC je A' , itd.. Dva nožišta sigurno leže na jednom pravcu,uzmem da su to B' i C', odredim sjecište pravca B'C' i treće stranice trokuta (stranice BC), neka je to A', spojim A' s onom proizvoljnom točkom na kružnici (recimo P) i treba sad dokazat da je pravac PA' visina na BC tj da je to pravi kut??? ugl nisam uspjela ništa dobit...jesam fulala u postavljanju zad? ispričavam se što je ovako opširno.
|
|
| [Vrh] |
|
|










