|
[quote="Gia"]
Odredi sve moguce vrijednosti integrala
[latex]
\int_\gamma \frac{dz}{z(z^2 -1)} \
[/latex]
za razlicite konture [latex] \gamma[/latex] koje ne prolaze ni jednom od tocaka 0, 1 i -1.
[/quote]
Da [latex]\gamma[/latex] ne prolazi tockama 1, -1 i 0 znaci tocno to sto kaze. Radi se u kompleksnoj ravnini -- dakle nesto tipa kruznica oko nule radijusa [latex]{1\over 2}[/latex].
Primjenjujemo teorem o residuumima.
Dakle, [latex]\gamma[/latex] moze obilaziti niti jednu od tih tocaka. Tada je integral 0, jer je funkcija ocito holomorfna u cijeloj kompleksnoj ravnini bez 0,1,-1.
Neka je [latex]f(z)={1\over z(z^2-1)}[/latex]
Racunamo residuume.
U tocki 0 razvucemo funkciju u red
[latex]
\eqalign{
f(z)&={1\over z}{1\over z-1}{1\over z+1}\cr
&={1\over z}\left({-\sum\limits_{n\geq0}z^n}\right)\left({\sum\limits_{n\geq0}(-z)^n}\right)\cr
&=-{1\over z}+\cdots\cr
}[/latex]
Pa znamo da je residuum u 0 jednak 1 (sjeti se, Residuum je koeficijent uz -1. clan Laurentovog reda).
Neka je sada [latex]y:=z-1[/latex], pa racunamo residuum u 1.
[latex]
\eqalign{
f(z)&={1\over z}{1\over z-1}{1\over z+1}\cr
&={1\over y+1}{1\over y}{1\over y+2}\cr
&={1\over y+1}{1\over y}{1\over 2\left({1\over 2}y+1\right)}\cr
&={1\over 2}{1\over y}\left({\sum\limits_{n\geq0}(-y)^n}\right)\left({\sum\limits_{n\geq0}\left({-y\over 2}\right)^n}\right)\cr
&={1\over 2}{1\over y}+\cdots\cr
}[/latex]
Dakle, u 1 je residuum [latex]{1\over 2}[/latex].
Jos je ostalo -1.
Neka je sada [latex]w:=z+1[/latex], pa racunamo residuum u 1.
[latex]
\eqalign{
f(z)&={1\over z}{1\over z-1}{1\over z+1}\cr
&={1\over w-1}{1\over w-2}{1\over w}\cr
&={1\over 1-w}{1\over w}{1\over 2\left(1-{1\over 2}w\right)}\cr
&={1\over 2}{1\over w}\left({\sum\limits_{n\geq0}(w)^n}\right)\left({\sum\limits_{n\geq0}\left({w\over 2}\right)^n}\right)\cr
}[/latex]
Dakle, i u -1 je residuum jednak [latex]{1\over 2}[/latex].
E, sad:
Imamo 8 mogucnosti, (zapravo 16, jer nije odredjen smjer), za svaki od polova po dvije ([latex]\top[/latex] ako obilazi pol, [latex]\bot[/latex] ako ne).
[latex]$
\halign{
\strut\hfill#\hfill&\hfill#\hfill&\hfill#\hfill&#\vrule&\hfill#\hfill\cr
$0$&$-1$&$1$&&$\int_\gamma f$\cr
\qquad&\qquad&\qquad&&\qquad\cr
\noalign{\vskip-12pt\hrule}
$\bot$&$\bot$&$\bot$&&$0$\cr
$\bot$&$\bot$&$\top$&&${1\over 2}$\cr
$\bot$&$\top$&$\bot$&&${1\over 2}$\cr
$\bot$&$\top$&$\top$&&$1$\cr
$\top$&$\bot$&$\bot$&&$-1$\cr
$\top$&$\bot$&$\top$&&$-{1\over 2}$\cr
$\top$&$\top$&$\bot$&&$-{1\over 2}$\cr
$\top$&$\top$&$\top$&&$0$\cr
}$[/latex]
Ovo je samo za jedan prolaz oko svakog pola. Opcenito, ako je [latex]
\nu_z[/latex] broj obilazenja krivulje [latex]\gamma[/latex] oko pola [latex] z[/latex], tada je
[latex]\displaystyle \int_\gamma {1\over z(z^2-1)}={1\over 2}\left({\nu_{-1}+\nu_1}\right)-\nu_0[/latex]
'ave fun!
Sinisa
| Gia (napisa): |
Odredi sve moguce vrijednosti integrala
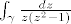
za razlicite konture 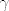 koje ne prolaze ni jednom od tocaka 0, 1 i -1. koje ne prolaze ni jednom od tocaka 0, 1 i -1.
|
Da 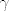 ne prolazi tockama 1, -1 i 0 znaci tocno to sto kaze. Radi se u kompleksnoj ravnini – dakle nesto tipa kruznica oko nule radijusa ne prolazi tockama 1, -1 i 0 znaci tocno to sto kaze. Radi se u kompleksnoj ravnini – dakle nesto tipa kruznica oko nule radijusa 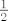 . .
Primjenjujemo teorem o residuumima.
Dakle, 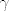 moze obilaziti niti jednu od tih tocaka. Tada je integral 0, jer je funkcija ocito holomorfna u cijeloj kompleksnoj ravnini bez 0,1,-1. moze obilaziti niti jednu od tih tocaka. Tada je integral 0, jer je funkcija ocito holomorfna u cijeloj kompleksnoj ravnini bez 0,1,-1.
Neka je 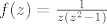
Racunamo residuume.
U tocki 0 razvucemo funkciju u red
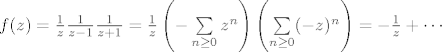
Pa znamo da je residuum u 0 jednak 1 (sjeti se, Residuum je koeficijent uz -1. clan Laurentovog reda).
Neka je sada 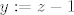 , pa racunamo residuum u 1. , pa racunamo residuum u 1.
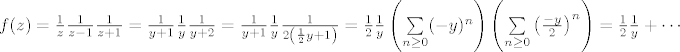
Dakle, u 1 je residuum 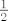 . .
Jos je ostalo -1.
Neka je sada 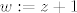 , pa racunamo residuum u 1. , pa racunamo residuum u 1.
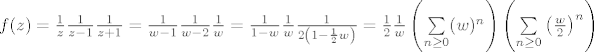
Dakle, i u -1 je residuum jednak 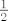 . .
E, sad:
Imamo 8 mogucnosti, (zapravo 16, jer nije odredjen smjer), za svaki od polova po dvije (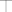 ako obilazi pol, ako obilazi pol, 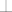 ako ne). ako ne).
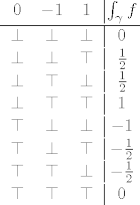
Ovo je samo za jedan prolaz oko svakog pola. Opcenito, ako je 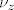 broj obilazenja krivulje broj obilazenja krivulje 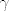 oko pola oko pola  , tada je , tada je
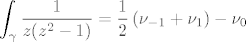
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|





