|
1. zadatak
[latex]\lim_{x\to0}\frac{(1+x^2)e^{\frac{3}{2}x^2}-1}{x\sin2x}[/latex] [latex]=\lim_{x\to0}\frac{(1+x^2)(e^{\frac{3}{2}x^2}-1)+1+x^2-1}{x\sin2x}[/latex] [latex]
=\lim_{x\to0}\frac{(1+x^2)\frac{(e^{\frac{3}{2}x^2}-1)}{\frac{3}{2}x^2}\cdot\frac{3}{2}x^2+x^2}{x\sin2x}[/latex] [latex]=\lim_{x\to0}\frac{(1+x^2)\cdot A(x)\cdot\frac{3}{2}x^2+x^2}{x\sin2x}[/latex] [latex]=\lim_{x\to0}\frac{(\frac{3}{2}(1+x^2)\cdot A(x)+1)x^2}{x\sin2x}[/latex] [latex]=\lim_{x\to0}\frac{\frac{3}{2}(1+x^2)\cdot A(x)+1}{\frac{\sin2x}{x}}
[/latex] [latex]=\lim_{x\to0}\frac{\frac{3}{2}(1+x^2)\cdot A(x)+1}{\frac{\sin2x}{2x}\cdot2}[/latex] [latex]=\frac{\frac{3}{2}\cdot(1+0^2)\cdot1+1}{1\cdot2}[/latex] [latex]=\frac{\frac{3}{2}+1}{2}=\frac{5}{4}[/latex], gdje je A(ž):=(e^ž-1)/ž . Naravno, limes funkcije A u nuli jednak je 1 , što smo iskoristili prilikom računanja našeg limesa. Vidi i dolje za neke važne napomene o tome.
2. zadatak
[latex]\lim_{x\to1}\frac{e^x-e}{\ln x}[/latex] [latex]=\lim_{y\to0}\frac{e\cdot\frac{e^y-1}{y}}{\frac{\ln(y+1)}{y}}[/latex] [latex]=\frac{e\cdot1}{1}=e[/latex]
3. zadatak
[latex]\lim_{x\to0}\frac{\cos3x\cdot e^{3x^2}-1}{\sin^2x}[/latex] (*kako si i ti krenuo*) [latex]=\lim_{x\to0}\frac{\cos3x(e^{3x^2}-1)+\cos3x-1}{\sin^2x}[/latex] [latex]=\lim_{x\to0}\frac{\cos3x\cdot\frac{e^{3x^2}-1}{3x^2}\cdot3+\frac{\cos3x-1}{(3x)^2}\cdot9}{(\frac{\sin x}{x})^2}[/latex] [latex]=\frac{1\cdot1\cdot3+(-\frac{1}{2}\cdot9}{1^2}=3-\frac{9}{2}=-\frac{3}{2}[/latex]
A sad malo o načinu računanja. Kao što si vjerojatno uočio, stvar je supstitucijom (najčešće translacijom ili recipročnom vrijednošću ako se radi o [latex]\infty[/latex] svesti varijablu limesa (recimo x ) da teži u nulu, i nakon toga izgraditi (množenjem/dijeljenjem i zbrajanjem/oduzimanjem prikladnih izrazâ) dani izraz od puno malih "cigala", koje su uglavnom dva tipa: ili izrazi koji su vrijednosti neprekidnih funkcijâ od x (na primjer ovaj 1+x^2 , ili cos3x , gore), pa su im limesi pri x->0 jednaki funkcijskim vrijednostima za x=0 , ili pak neki od "tabličnih" dobro poznatih izraza čije limese u nuli znamo, npr. (e^x-1)/x , sinx/x , ln(1+x)/x , (cosx-1)/x^2 itd. [size=9](Ima tu još nekih trikova, no pomoću ovih se može riješiti velik broj zadataka.)[/size]
(e sad dolazi važan dio) [b]Nakon toga[/b], nakon što smo stvar kompletno napisali pomoću dobrih računskih operacijâ i gore navedenih građevnih blokova, _tada_ primjenjujemo teoreme o limesima da zaključimo da limes toga postoji, i da je jednak izrazu u koji se na mjesto danih građevnih blokova uvrste njihovi limesi. _Svi odjednom_ - to je kritično.
Vidim gore da pišeš, i nažalost nisi jedini (vidjeh mnoge da su to isto radili na kolokviju iz analize), u stilu,
lim...blabla...([color=red](e^2x-1)/2x[/color]*2+[color=blue]3x[/color])/...blabla...=
=lim...blabla...([color=red]1[/color]*2+[color=blue]3x[/color])/...blabla...
, odnosno da _pod limesom_ zamjenjuješ _neke_, ali ne sve (primijeti plavi 3x koji je ostao čekati neke bolje dane), funkcije varijable x , njihovim limesima. [b]To nije matematički opravdano[/b], i lako može dovesti do pogrešnih rezultatâ. Evo primjera koji je namjerno banalan da se lakše uoči greška (nije ga problem zakomplicirati), ali je razmišljanje istog tipa:
Imam [latex]\lim_{x\to0}\frac{x}{x}[/latex]. Naravno, funkcija pod limesom jednaka je svuda osim u 0 konstanti 1 , pa je i njen limes jednak limesu konstante 1 u 0 , dakle 1 . [b]No[/b], kad bih na to primijenio gornje razmišljanje, mogao bih reći: aha, ovaj gornji x mi ide u 0 , dakle mogu njega zamijeniti s 0 i računati limes dalje...
U tom slučaju, dobio bih [latex]\lim_{x\to0}\frac{0}{x}[/latex], no sad je funkcija pod limesom svuda osim u 0 jednaka konstanti _0_, te je i limes jednak 0. Ukratko, dobio bih glupost. Zašto?
Otprilike (na MA3 naučit ćete više), zato što ne mogu razlikovati pojedine x-eve pod limesom. Operator limesa je gore jedan jedini, i kaže da _svi_ x-evi koji se pojavljuju u izrazu pod limesom, moraju simultano i jednako težiti k 0 (ili čemu već). Ne mogu jedne već zamijeniti njihovim limesima, a druge ne. Tj. mogu, ako mi je funkcija u pitanju neprekidna kao _funkcija više varijabli_. No to nije isti pojam kao neprekidnost funkcije jedne varijable, i s razlogom je njegovo žvakanje ostavljeno za drugu godinu. Zasad samo treba znati da gornje razmišljanje ne valja, i može dovesti do krivih rezultata.
Kako onda treba razmišljati? Naravno, bilo bi idealno svaki od tih malih izraza pisati svaki put iznova kad neki drugi dio limesa želimo raspisati, no to bi, ako ne planiramo jako dobro, ubrzo dovelo do ogromne redundancije, i još do ogromnih izraza u kojima bismo se teško snašli. Jedno od rješenja je uvesti funkcijsku supstituciju, kao što sam ja gore napravio u rješenju prvog zadatka. Primijeti: kad mi se pojavio (e^(3/2*x^2)-1)/(3/2*x^2) , nisam ga išao prepisivati kasnije (puno bespotrebnog posla, ali korektno), niti sam ga zamijenio njegovim limesom u nuli, brojem 1 ([b]netočno![/b]), već sam uveo novo slovo i označio ga s A(x) . Znajući da mi je [latex]\lim_{x\to0}A(x)=1[/latex], ali isto tako znajući da tu zamjenu ( A(x) sa 1 ) mogu izvesti tek na kraju, kad složim sve ostale građevne blokove na svoja mjesta, i riješim se znaka [latex]\lim[/latex] ispred.
Jasnije?
1. zadatak
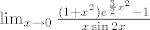 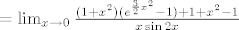 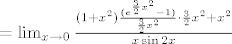 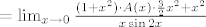 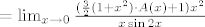 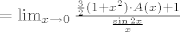 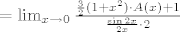 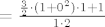 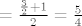 , gdje je A(ž):=(e^ž-1)/ž . Naravno, limes funkcije A u nuli jednak je 1 , što smo iskoristili prilikom računanja našeg limesa. Vidi i dolje za neke važne napomene o tome. , gdje je A(ž):=(e^ž-1)/ž . Naravno, limes funkcije A u nuli jednak je 1 , što smo iskoristili prilikom računanja našeg limesa. Vidi i dolje za neke važne napomene o tome.
2. zadatak
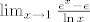 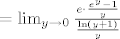 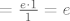
3. zadatak
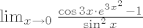 (*kako si i ti krenuo*) (*kako si i ti krenuo*) 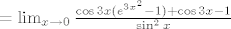 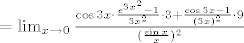 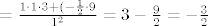
A sad malo o načinu računanja. Kao što si vjerojatno uočio, stvar je supstitucijom (najčešće translacijom ili recipročnom vrijednošću ako se radi o 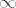 svesti varijablu limesa (recimo x ) da teži u nulu, i nakon toga izgraditi (množenjem/dijeljenjem i zbrajanjem/oduzimanjem prikladnih izrazâ) dani izraz od puno malih "cigala", koje su uglavnom dva tipa: ili izrazi koji su vrijednosti neprekidnih funkcijâ od x (na primjer ovaj 1+x^2 , ili cos3x , gore), pa su im limesi pri x→0 jednaki funkcijskim vrijednostima za x=0 , ili pak neki od "tabličnih" dobro poznatih izraza čije limese u nuli znamo, npr. (e^x-1)/x , sinx/x , ln(1+x)/x , (cosx-1)/x^2 itd. (Ima tu još nekih trikova, no pomoću ovih se može riješiti velik broj zadataka.) svesti varijablu limesa (recimo x ) da teži u nulu, i nakon toga izgraditi (množenjem/dijeljenjem i zbrajanjem/oduzimanjem prikladnih izrazâ) dani izraz od puno malih "cigala", koje su uglavnom dva tipa: ili izrazi koji su vrijednosti neprekidnih funkcijâ od x (na primjer ovaj 1+x^2 , ili cos3x , gore), pa su im limesi pri x→0 jednaki funkcijskim vrijednostima za x=0 , ili pak neki od "tabličnih" dobro poznatih izraza čije limese u nuli znamo, npr. (e^x-1)/x , sinx/x , ln(1+x)/x , (cosx-1)/x^2 itd. (Ima tu još nekih trikova, no pomoću ovih se može riješiti velik broj zadataka.)
(e sad dolazi važan dio) Nakon toga, nakon što smo stvar kompletno napisali pomoću dobrih računskih operacijâ i gore navedenih građevnih blokova, _tada_ primjenjujemo teoreme o limesima da zaključimo da limes toga postoji, i da je jednak izrazu u koji se na mjesto danih građevnih blokova uvrste njihovi limesi. _Svi odjednom_ - to je kritično.
Vidim gore da pišeš, i nažalost nisi jedini (vidjeh mnoge da su to isto radili na kolokviju iz analize), u stilu,
lim...blabla...((e^2x-1)/2x*2+3x)/...blabla...=
=lim...blabla...(1*2+3x)/...blabla...
, odnosno da _pod limesom_ zamjenjuješ _neke_, ali ne sve (primijeti plavi 3x koji je ostao čekati neke bolje dane), funkcije varijable x , njihovim limesima. To nije matematički opravdano, i lako može dovesti do pogrešnih rezultatâ. Evo primjera koji je namjerno banalan da se lakše uoči greška (nije ga problem zakomplicirati), ali je razmišljanje istog tipa:
Imam 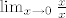 . Naravno, funkcija pod limesom jednaka je svuda osim u 0 konstanti 1 , pa je i njen limes jednak limesu konstante 1 u 0 , dakle 1 . No, kad bih na to primijenio gornje razmišljanje, mogao bih reći: aha, ovaj gornji x mi ide u 0 , dakle mogu njega zamijeniti s 0 i računati limes dalje... . Naravno, funkcija pod limesom jednaka je svuda osim u 0 konstanti 1 , pa je i njen limes jednak limesu konstante 1 u 0 , dakle 1 . No, kad bih na to primijenio gornje razmišljanje, mogao bih reći: aha, ovaj gornji x mi ide u 0 , dakle mogu njega zamijeniti s 0 i računati limes dalje...
U tom slučaju, dobio bih 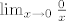 , no sad je funkcija pod limesom svuda osim u 0 jednaka konstanti _0_, te je i limes jednak 0. Ukratko, dobio bih glupost. Zašto? , no sad je funkcija pod limesom svuda osim u 0 jednaka konstanti _0_, te je i limes jednak 0. Ukratko, dobio bih glupost. Zašto?
Otprilike (na MA3 naučit ćete više), zato što ne mogu razlikovati pojedine x-eve pod limesom. Operator limesa je gore jedan jedini, i kaže da _svi_ x-evi koji se pojavljuju u izrazu pod limesom, moraju simultano i jednako težiti k 0 (ili čemu već). Ne mogu jedne već zamijeniti njihovim limesima, a druge ne. Tj. mogu, ako mi je funkcija u pitanju neprekidna kao _funkcija više varijabli_. No to nije isti pojam kao neprekidnost funkcije jedne varijable, i s razlogom je njegovo žvakanje ostavljeno za drugu godinu. Zasad samo treba znati da gornje razmišljanje ne valja, i može dovesti do krivih rezultata.
Kako onda treba razmišljati? Naravno, bilo bi idealno svaki od tih malih izraza pisati svaki put iznova kad neki drugi dio limesa želimo raspisati, no to bi, ako ne planiramo jako dobro, ubrzo dovelo do ogromne redundancije, i još do ogromnih izraza u kojima bismo se teško snašli. Jedno od rješenja je uvesti funkcijsku supstituciju, kao što sam ja gore napravio u rješenju prvog zadatka. Primijeti: kad mi se pojavio (e^(3/2*x^2)-1)/(3/2*x^2) , nisam ga išao prepisivati kasnije (puno bespotrebnog posla, ali korektno), niti sam ga zamijenio njegovim limesom u nuli, brojem 1 (netočno!), već sam uveo novo slovo i označio ga s A(x) . Znajući da mi je 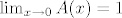 , ali isto tako znajući da tu zamjenu ( A(x) sa 1 ) mogu izvesti tek na kraju, kad složim sve ostale građevne blokove na svoja mjesta, i riješim se znaka , ali isto tako znajući da tu zamjenu ( A(x) sa 1 ) mogu izvesti tek na kraju, kad složim sve ostale građevne blokove na svoja mjesta, i riješim se znaka 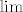 ispred. ispred.
Jasnije?
|









